• Home
  • About
    • 검은색 잉크 블로그 photo

      검은색 잉크 블로그

      github GIST → https://gist.github.com/BlaCkinkGJ입니다.

    • Learn More
    • Email
    • Github
  • Posts
    • All Posts
    • All Tags
  • Projects

[운영체제] 페이징(Paging)

14 Jan 2020

Reading time ~7 minutes

출처 : http://pages.cs.wisc.edu/~remzi/OSTEP/

이 게시글은 2018년에 작성한 내용을 복구한 것으로 원문은 개정되었을 수 있으니 참고 바랍니다.

Paging

Paging

지난 시간의 Fragmentation(이하 파편화) 기법을 보완하기 위해 나온 방법이 바로 Paging(이하 페이징) 방법입니다. 이 방법은 논리적인 Segment(이하 세그먼트)들로 가변 크기로 나누는 세그멘테이션에 비해 주소 공간을 페이지라고 불리는 정해진 크기로 쪼개는 것입니다. 이런 페이징을 통해 물리적 메모리는 페이지들을 나눈 결과인 페이지 프레임으로 만들 수 있습니다. 이런 값은 페이지 테이블을 통해서 가상 주소를 물리적 주소로 변경할 수 있게 됩니다.

이런 페이징을 할 때에는 동일 크기의 블럭으로 가상 메모리를 나누어야 합니다.(페이지) 그리고 고정된 크기의 메모리로 물리적 크기를 나누게 됩니다.(프레임) 이렇게 만들어지는 페이지의 크기는 2의 승수가 되어야 합니다. 이를 위해 OS는 모든 사용가능한 프레임을 알고 있어야 합니다. 또한 n 개의 페이지를 가지는 프로그램을 돌리기 위해서는 n 개 프레임이 있어야 프로그램을 가져올 수 있습니다. 이를 하는 데에는 앞에서 이야기한 페이지 테이블을 통해 수행을 하고, 이 방법은 외부 파편화를 방지 할 수 있습니다. 그리고 이런 페이지는 주소 공간의 추상화를 함으로 유연한 메모리 관리를 할 수 있고, 빈 공간의 관리를 간단하게 할 수 있습니다.

이런 페이징을 위한 가상 주소는 크게 VPN(Virtual Page Number)과 Offset으로 구성됩니다. VPN은 페이지 테이블의 index 역할을 합니다. 이와 같이, 물리 주소는 PFN(Page Frame Number)과 Offset으로 구성됩니다. 그리고 페이지 테이블은 OS에서 관리되며, VPN을 PFN으로 바꾸는 역할을 합니다. 그리고 가상 주소 공간에서의 하나의 페이지는 하나의 PTE(Page Table Entry)를 가집니다. 이런 페이징 방법은 아래 그림과 같이 동작 합니다.

예를 들어, 다음과 같은 기계가 있다고 가정하겠습니다.

  • Virtual address: 32 bits
    • VPN: 20 bits
    • Offset: 12 bits
  • Physical address: 20 bits
  • Page size: 4KB
  • Page table entries: \(\)2^{20}\(\)

여기서 우리는 상단의 Virtual Address와 Physical Address, Page Size를 바탕으로 하단의 값들을 구할 수 있어야 합니다. 이는 아래와 같은 식에 의해 유도 됩니다.

\[offset = \log_2{(page\:size)(=\log_22^{12})}\] \[VPN = Virtual\:Addres - offset\] \[Page\:Table\:Entry = 2^{(VPN)}\] \[Page\:Table\:Size = Page\:Table\:Entry(2^{20}) \times Entry\:Size(1) = 2^{20}\]

여기서 Entry Size가 1인 이유는 위의 Page Table Entry의 값을 보면 0xA4와 같이 되어 있습니다. 이는 8bits이고 해당 연산은 Byte를 기준으로 하기 때문에 1이 Entry Size가 됩니다. 아래가 Paging 방법으로 메모리에 접근하는 코드입니다.

VPN     = (VirtualAddress & VPN_MASK) >> SHIFT;
// Form the address of the page-table entry(PTE)
// PTBR → Page Table Base Register
PTEAddr = PTBR + (VPN * sizeof(PTE));
PTE     = AccessMemory(PTEAddr);

if(PTE.Valid == False)
  RaiseException(SEGMENTATION_FAULT);
else if (CanAccess(PTE.ProtectBits) == FALSE)
  RaiseException(PROTECTION_FAULT);
else
  offset   = VirtualAddress & OFFSET_MASK;
  PhyAddr  = (PTE.PFN << PFN_SHIFT) | offset;
  Register = AccessMemory(PhysAddr)

이 코드에 의해서 아래의 코드를 동작을 시킨다고 가정할 때의 메모리의 동작을 확인해보도록 하겠습니다.

int array[1000];
for(i = 0; i < 1000; i++)
  array[i] = 0;

이 코드를 어셈블리어로 변경하면 아래와 같이 됩니다.

0x1024 movl $$0x0, (%edi, %eax, 4)
0x1028 incl %eax
0x102c cmpl $$0x03e8, %eax
0x1030 jne  0x1024

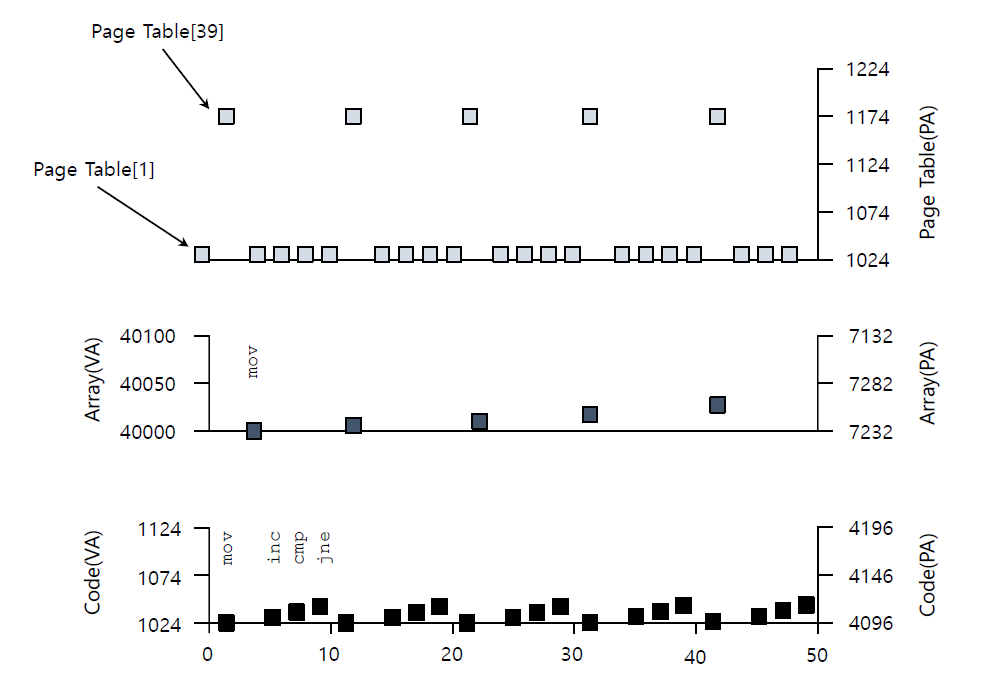
위의 코드를 돌리면 아래와 같은 메모리 접근 상태가 보입니다.

Memory Access

그리고 Demand Paging 기법이 있습니다. 이 방법은 swap하고 cache를 알아야 합니다. 이 방법은 process가 전혀 자신의 메모리 상황이 어떻게 돌아가는 지 알 수 없게 합니다. 이런 방식의 이점은 아래와 같습니다.

  • I/O가 적게 필요합니다.

  • 메모리가 적게 필요합니다.

  • 더 빠른 반응 속도를 지원합니다.

  • 더 많은 프로세스들을 지원합니다.

또한 잘못된 PTE를 접근을 할 때, CPU가 발생시키는 Page Fault가 있습니다. 이런 Page Fault는 실제로 메모리가 없는 경우에 발생하는 Major page faults가 있고, 다른 프로세스의 사용으로 사용이 불가능한 경우인 Minor Page Fault가 있습니다. 전자의 대표적인 예로 Require disk I/O상태가 있고, 후자의 예로는 아직 Fetch가 되지 않은 페이지를 접근하는 경우가 있을 수 있습니다.

결론적으로, 페이징 방법을 정리하면 장점으로는 ▲ 외부 파편화가 발생하지 않는다. ▲ 할당과 해제가 빠르다. ▲페이지가 분할 되어 있으므로 쉽게 최소의 I/O 작업을 통해 메모리로 값을 가져올 수 있습니다. ▲ 페이지를 쉽게 공유하고 보호할 수 있습니다. 하지만 단점으로는 ▲ 메모리를 접근할 때마다 PTE를 참고해야 하기 때문에 너무 느립니다. ▲ 내부 파편화가 발생합니다. ▲ 페이지 테이블을 저장하기 위해 소모되는 공간이 너무 큽니다.

Translation Lookaside Buffers (TLBs)

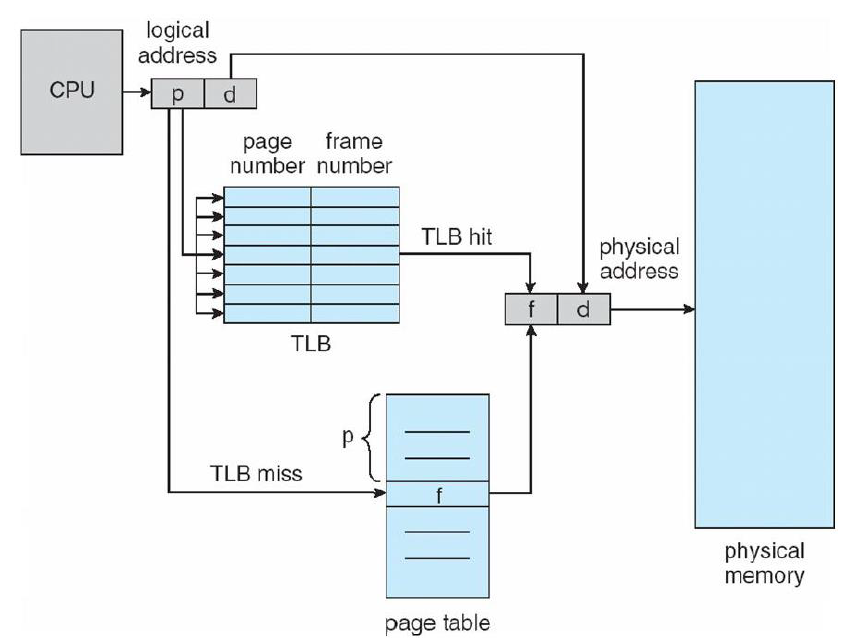
이 방법은 위에서 언급한 단점 중 시간 소모를 줄이는 방법과 관련이 있습니다. Memory Management Unit(이하 MMU)를 사용하는 방법입니다. 이 방법은 자주 사용하는 주소를 하드웨어의 캐시에 넣는 방법 입니다. TLB 방법은 컴퓨터 구조에서 캐시 내용 중 Fully Associative와 관련이 있습니다. 그리고 전환 정책은 LRU(마지막으로 사용된 시간이 가장 오래된 것을 제거하는 방식)에 해당합니다. 주의사항으로 TLB는 PTE를 캐시에 넣는 방법이지 PFN을 넣는 방법이 아닙니다. TLB의 동작은 아래와 같습니다.

TLB

이런 TLP는 Loop와 같은 가까운 위치에 있는 데이터를 꺼낼 때 효율적입니다. 그리고 Locality라는 용어가 있습니다. Locality는 크게 Temporal Locality와 Spatial Locality로 나뉩니다. 전자는 최근에 접근한 곳이 나중에 접근할 가능성이 높다는 의미로 사용이 되고, 후자는 가상 메모리에서 어느 위치에서 접근을 하면 다음 동작은 그 위치 주변 메모리를 가져온다는 것을 의미합니다.

근데 이 방법에 문제가 있습니다. Context Switching(이하 문맥 교환)을 하는 경우에 TLB Table에 각 프로세스의 VPN이 똑같으면 충돌이 발생하게 됩니다. 이 문제를 해결하기 위해 먼저 문맥 교환을 할 때 마다 지우는 방법을 사용하도록 합니다. 이 방법은 지우고 쓰고 하면서 비용이 많이 들며 TLB를 사용하는 이유 조차 퇴색시킵니다. 다른 방법으로는 Address Space Identifier(ASID)를 두는 방법입니다. 이 방법은 각각의 프로세스에 고유 ID 값을 주어 구분을 하는 방법입니다.

또 다른 문제로는 두 개의 프로세스가 페이지 프레임을 공유하는 경우가 있습니다. 이 경우 해결 방법은 VPN을 서로 다르게 하여 연결을 하도록 합니다.

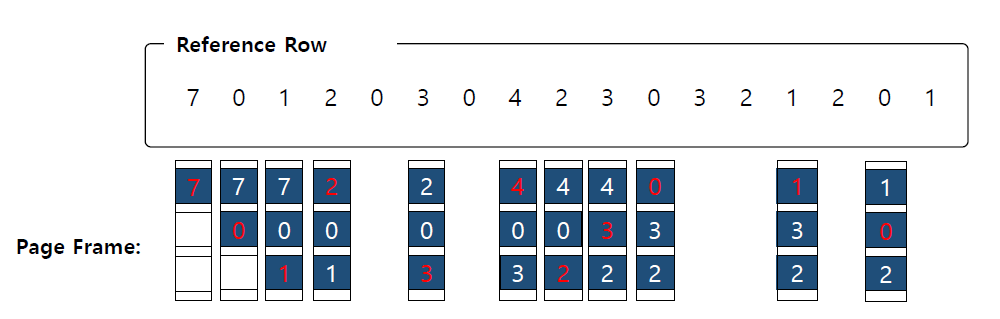
TLB의 캐시 데이터의 교환 정책은 앞서 언급하였듯이 LRU입니다. 이러한 LRU가 어떻게 동작을 하는 지 아래의 그림을 통해 알아보도록 하겠습니다.

TLB Policy

이는 총 11번 TLB miss가 나는 예제 입니다. 여기서 유의해야 할 점은 최근에 hit가 있는 놈의 Counter는 0이 되는 것입니다. 이에 따라, 앞의 701203에서 0이 hit이므로 3이 다음에 들어갈 때 1이 지워지는 것을 볼 수 있습니다.

결과적으로, 이러한 TLB의 성능은 컴퓨터 전체의 성능에 영향을 주게 됩니다. 그러므로 TLB hit가 잘 이루어질 수 있도록 TLB가 관리하는 영역을 키우고, TLB에 친화적인 알고리즘을 작성하도록 해야합니다.

Smaller Tables

위에서 언급한 단점 중 공간 소모를 줄이는 방법과 관련이 있습니다. 이전의 페이징은 모든 프로세스가 하나의 페이지를 각각 가지고 있어야 했습니다. 만약 32-bit address에 4KB pages와 4-byte page-table entry라고 가정을 하면 아래와 같은 크기가 나오게 됩니다.

\[Page\:Table\:Size = \dfrac{2^{32}}{2^{12}}*4 = 2^{22} = 4MB\]

이는 심지어 프로세스 하나 당에 해당합니다. 만약 프로세스가 100개만 돌아가도 페이지 테이블 크기에만 400MB를 사용하게 됩니다. 따라서 이를 줄일 필요가 있습니다.

첫 번째 방법은 애초에 페이지의 크기를 키워버리는 것입니다. 기존 4KB의 페이지 크기를 16KB로 바꿔버리면 됩니다. 하지만 이 방법은 아무래도 문제 있는 Internal Fragmentation을 추가로 너 만드는 것이므로 절대 효율적인 방법은 아니게 됩니다. 이에 따라 새로운 방법을 찾을 필요가 있게 되었습니다.

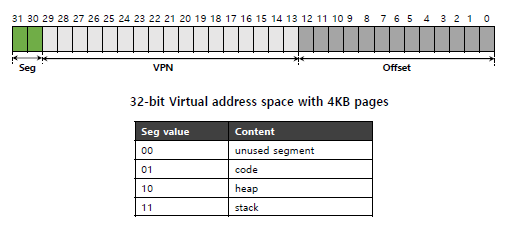
결과적으로, 페이징 기법과 세그먼트 기법을 융합한 방법을 사용하게 되었습니다.이는 페이지 테이블을 일정 세그먼트 단위로 잘라서 사용하는 방법입니다. 이 세그먼트는 물리 주소 공간에서의 세그먼트가 아니라 페이지 테이블의 세그먼트를 의미 합니다. 이런 방식에 따라 어떤 32-bit address에서의 가상 주소는 아래와 같은 모양을 가집니다.

Hybrid Approach

이전의 모형과 다른점은 Seg 항목이 추가된 점입니다. 만약 TLB hit가 성공한 경우는 사실 이 부분을 신경 쓸 필요가 없습니다. 하지만 TLB miss인 경우 이는 동작하게 됩니다. 이 경우 아래와 같은 방식으로 각 정보를 가져오게 됩니다.

SN = (VirtualAddress & SEG_MASK) >> SN_SHIFT
VPN = (VirtualAddress & VPN_MASK) >> VPN_SHIFT
AddressOfPTE = Base[SN] + (VPN * sizeof(PTE))

하지만 이 방법도 문제가 있게 됩니다. 만약 엄청 크게 크기를 잡아 놓았는 데 프로세스가 거의 사용하지 않는다면, 결국 이 또한 페이지 테이블의 낭비를 일으키게 됩니다.

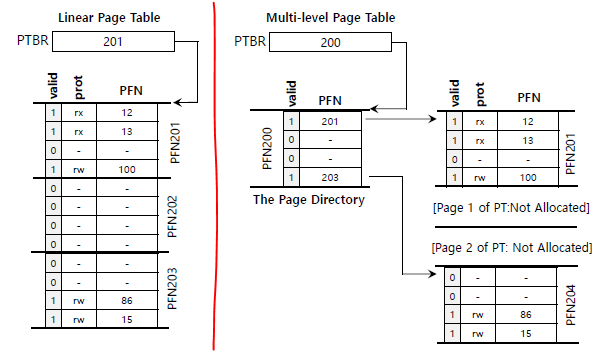
이를 해결하기 위해 나온 방법이 Multi-Level Page Table 방법 입니다. 이게 현대의 OS에서 사용하는 방식과 유사 합니다. 이 방식은 Page Directory(이하 페이지 디렉토리)라는 것을 사용하는 데 이를 통하면 찾기가 약간은 힘들기는 하지만 공간을 많이 절약을 할 수 있다는 장점이 있습니다. 페이지 디렉토리의 동작은 아래와 같이 동작을 합니다. 왼쪽이 기존의 페이지 테이블 방법이고, 오른쪽이 Multi-Level Page Table 방법입니다.

Page Directory

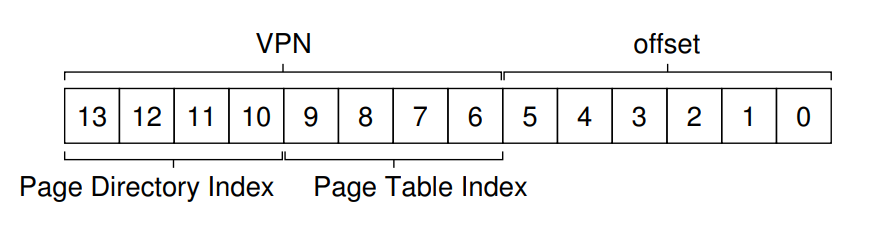
이 방식으로 만들어지는 Virtual Address는 아래와 같은 모양을 띕니다.

Virtual Address Memory

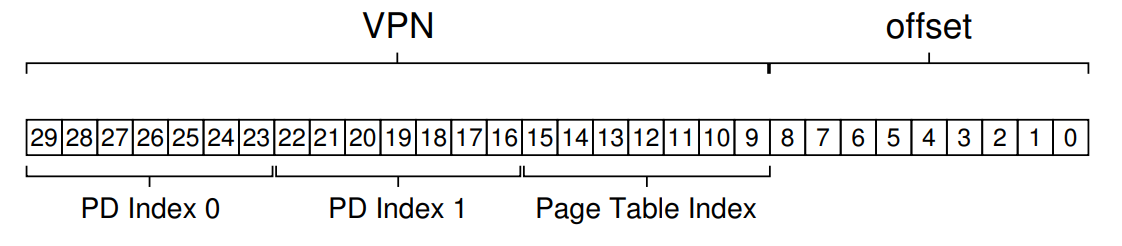
하지만 이 방식은 추가적으로 만약 저렇게 페이지 디렉토리 테이블이 하나만 만들어진다면 Double-Level 일텐데, 이름에서 Multi-Level에서 알 수 있듯이 여러 개의 Table을 더 만들 수 있습니다. 좀 더 레벨을 깊게 한다면 아래와 같은 가상 주소를 가지게 됩니다.

Multi!

이는 어떤 계산 값을 바탕으로 나오게 되냐면 먼저 조건을 주길

  • Page Table Entry Size = 4-byte(32bits)

  • Page Size = 512-byte

  • Each Directory = 16KB

  • Page Entry per page = 128 PTEs

이를 바탕으로 연산을 하면 아래와 같이 나옵니다.

\[PD\:size= PTE \times Page\:Directory = 2^2 \times 16KB = 2^{16}\] \[offset = \log_2(Page\:Size) = \log_22^{9} = 9\] \[Page\:Table\:Index = \log_22^7 = 7\] \[PD \:Index \:size = \log_2\dfrac{PD\:size}{offset}=\log_2\dfrac{2^{16}}{2^9}=log_22^7=7\]

그리고 Inverted Page Table이라는 것이 있습니다. 이것은 물리적 메모리에 페이지 테이블이 하나가 있고 이를 바탕으로 메모리에 접근을 하는 방식입니다. 이것의 장점은 페이지 테이블을 저장할 메모리가 감소한다는 것입니다. 단점으로는 시간이 추가적으로 더 필요하다는 것입니다.


ospaging Share Tweet +1