출처 : Willian Stallings. (2013). Computer Organization and Architecture. London:Pearson

Instruction Sets

Characteristic and Functions

명령어 집합(instructure set)은 CPU에 의해서 해설되는 명령어들의 집합을 지칭을 합니다. 일반적으로, 어셈블리 언어로 표현이 많이되나 상황에 따라서 2진 코드로 표현되기도 합니다. 이러한 명령어 집합의 명령어들은 아래와 같은 원소로 구성됩니다.

• opcode : Do this
• source operand : To this
• result operand : Put the answer here
• next instruction : When you have done that, do this…

이것들은 다음과 같은 Cycle에 의해 동작을 하게 됩니다.

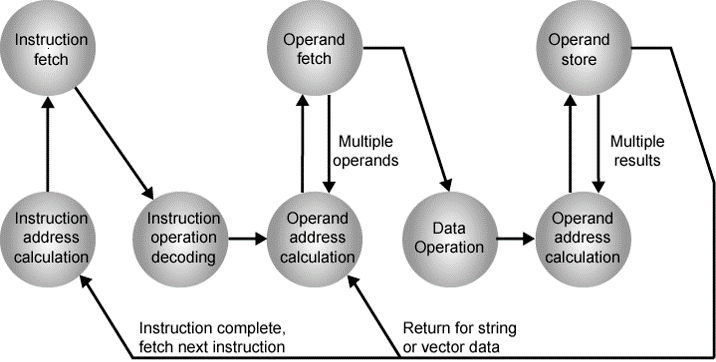
다음은 가장 간단한 주소의 모습입니다.

이런 명령어가 수행하는 것의 종류에는 4 가지가 존재합니다.

1. 데이터의 처리
2. 데이터의 저장
3. 데이터의 이동
4. 프로그램의 흐름 제어

그리고 이러한 주소는 피연산자(operand)의 갯수에 따라 0 에서 3 까지 지정됩니다.

3 addresses

피연산자의 주소를 담는 부분이 2개 존재를 하고 결과를 넣는 주소 공간이 1개 존재하는 주소 방식을 지칭합니다. 이는 흔한 방식은 아닙니다.

\[result = operand1 + operand2\]

2 addresses

피연산자의 주소가 2개이고 2개 중 1개를 result의 역할을 겸임을 하게 만들도록 합니다.

\[operand1 = operand1 + operand2\]

이 방법은 명령어의 길이를 줄일 수 있으며, 약간의 추가적인 작업이 요구됩니다.

1 address

이는 두 번째 주소가 함축된 방식입니다. 일반적으로 레지스터(Accumulator)에서 사용됩니다. 초창기의 컴퓨터에서 많이 사용하였습니다.

0 address

주소들은 묵시적으로 해석이되고, 스택의 자료 구조를 가집니다. 이러한 구조는 피연산자를 지니지 않으므로 명령어를 매우 짧게 만들 수 있는 장점이 있습니다. 하지만 속도가 느려지는 단점이 있습니다.

정리하면 주소를 많이 사용할 수록 명령어가 복잡해지고, 레지스터를 많이 사용하며, 프로그램 당 명령어의 갯수가 줄어듭니다. 이와 반대로 주소를 적게 사용하면 명령어가 덜 복잡해지고, 프로그램에 더욱 많은 명령어를 넣을 수 있고, 명령어를 Fetch/Execution을 하는 데에도 더욱 빠르게 진행할 수 있습니다.

잠시 논외로 이 책을 읽다보면 다음의 용어 Big-Endian이랑 Little-Endian이 있습니다. 이것을 잠시 집고 넘어가자면 이는 CPU가 데이터를 쓸 때 중요한 개념입니다. 0x12345678을 넣는다고 할 경우 전자는 12 34 56 78이 들어가게 되고, 후자는 78 56 34 12로 들어가게 됩니다. 이 들어가는 것은 바이트 단위로 들어가게 됩니다. 인텔 CPU는 후자를 따릅니다.

이러한 명령어들 중에 산술이나 저장, 읽기와 같은 명령어는 직관적으로 알 수 있습니다. 그 중 독특한 것으로 제어를 다루기 위한 것 3가지가 있는 데 이것을 한 번 확인해보도록 하겠습니다.

1. Branch : 이는 우리가 익히 아는 조건문에 따라 어디로 분기할 것이 관련된 명령어를 지칭합니다.
2. Skip : 이는 다음의 내용이나 지정된 내용을 넘기기위해 사용하는 것입니다. 예를 들어, 만약 0이 되면 다음 명령어를 무시하도록 하는 것이 있습니다. 이러한 명령을 수행하는 것으로 ISZ라고 있습니다. 이는 Increment operand and Skip next instruction if the result is Zero의 약자로 어떤 값이 0인 경우 명령어 위치를 가리키는 레지스터의 값을 증가시키는 역할을 합니다.
3. Subroutine Call : 인터럽트 호출 같은 것이 있습니다.

Addressing Modes and Formats

주소의 종류는 여러가지가 있는 데 대표적인 종류로 아래의 7개의 종류가 있습니다.

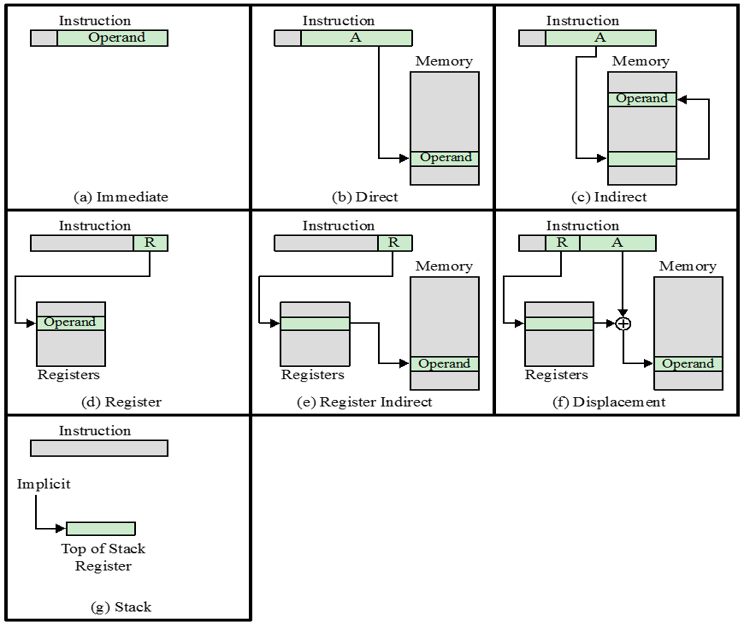
위의 그림에서 (b), (c) 중에서 속도가 빠른 것은 (b) 입니다. 왜냐하면 (c)는 추가적인 메모리 접근이 요구되지만 (b)는 그렇지 않기 때문입니다. 하지만 (b)는 (c)에 비해 접근 시 사용되는 비트가 제한되기 때문에 접근할 수 있는 주소 공간이 적습니다. 그리고 (f)에서 A, R가 있는 데 여기서 A는 기준점이고, R은 기준점에 대한 변위(displacement) 값이 됩니다. 각각 표로 정리하면 다음과 같습니다.

종류	알고리즘	장점	단점
Immediate	Operand = A	레퍼런스 없음	피연산자 크기 제한
Direct	EA = A	단순함	주소 공간 제한
Indirect	EA = (A)	많은 주소 공간	다중 메모리 참조
Register	EA = R	메모리 참조 없음	주소 공간 제한
Register Indirect	EA = (R)	많은 주소 공간	추가 메모리 참조
Displacement	EA = A + (R)	유연함	복잡함
Stack	EA = top of stack	메모리 참조 없음	응용 제한

여기서 EA는 Effective Address. 즉, 피연산자가 참조하는 내용의 주소를 의미합니다. 그리고 위에서 괄호가 많이 나오는 데 이 의미는 A에 가서 주소 값을 읽어서 간접 참조를 함을 의미합니다. 해석할 때 “~가 담고있는 주소의 내용은” 이라고 해석을 하면 될 것 같습니다.

Displacement Addressing

좀 더 변위 주소법에 관해서 알아보도록 하겠습니다. 이 표현법은 다른 말로 상대 주소법(Relatove Addressing)이라고도 합니다. 앞의 (f) 그림을 잘 참고해보면 R이 레지스터를 참고함을 알 수 있습니다. 이 R이 참조하는 것은 다름아니라 PC(Program Counter)를 참조합니다. 즉, 이를 사용하면 묵시적으로 위치를 값을 변경해갈 수 있는 장점이 있습니다.

여기서 기준 위치에서 다른 위치로 어느 일정한 값으로 움직이는 것을 Base-Register Addressing이라고 지칭하고, 그 변위의 값이 1씩 증가해서 값을 찾아가는 것을 Indexed Addressing이라고 합니다. 헌데 이를 하는 데 일반적인 방식으로는 덧셈 연산을 하므로, 그 속도가 느리므로 하드웨어적인 지원을 사용하는 것이 중요합니다. 이런 지원을 보고 Autoindexing이라고 합니다.

Autoindexing은 다음과 같은 순서로 실시됩니다.

1. 인덱스 수행 전 : 간접 주소 값을 얻은 후, 인덱스 값을 계산합니다.
2. EA = (A) + (R) 을 수행 : 이는 동일한 형태를 가지는 여러 블록을 처리하는 데 유용합니다.
3. 간접 주소 접근이 일어나기 전에 인덱싱이 완료됩니다.

이와 같은 방법으로 좀 더 효율적으로 명령을 수행할 수 있습니다.