• Home
  • About
    • 검은색 잉크 블로그 photo

      검은색 잉크 블로그

      github GIST → https://gist.github.com/BlaCkinkGJ입니다.

    • Learn More
    • Email
    • Github
  • Posts
    • All Posts
    • All Tags
  • Projects

[데이터베이스] 관계 데이터 모델

16 Oct 2018

Reading time ~6 minutes

개괄

관계 데이터 모델은 데이터베이스를 관계(relation)로 간주하는 것을 의미합니다. 여기서 관계는 테이블(table)을 의미하기도 합니다. 이는 매우 실세계를 자연스럽게 생각하는 방식으로 해석한 것이라고 볼 수 있습니다.

관계 모델의 기본

이러한 관계 데이터 모델은 수학 기호를 사용되어서 표시하도록 합니다. 이러한 수학적 표기를 도입하면 2가지 장점이 있습니다.

  1. 개념이 명확해진다.
  2. 증명이 가능해진다.

이러한 관계 데이터 모델에서 데이터베이스는 테이블의 집합으로 이야기됩니다. 이러한 테이블은 속성(Attributes) 간에 관계(\(R\))로 정의되는 아래와 같은 특징을 가집니다.

  1. 관계 \(R \subseteq A_1 \times A_2 ...\times A_n = \{(a_1, a_2,a_3,...,a_n) \mid a_i \in A_i\}\)
  2. \(A_i\): 속성(attribute) 또는 도메인(domain), 필드(field)
  3. \(a_i\): 속성 값
  4. 스키마(schema): \(R(A_1, A_2, ..., A_n)\)
  5. 튜플(tuple): \((a_1, a_2, a_3, ..., a_n)\)

다음으로 스키마라하는 것은 관계의 이름과 속성들의 집합을 지칭합니다. 이러한 스키마는 데이터베이스 골격을 만드는 데 중요한 역할을 합니다. 만약 학생에 관한 관계를 만든다고 해보겠습니다. 이 경우 속성으로는 성별, 학년, 학과가 있을 수 있습니다. 이를 스키마로 표현하면 아래와 같이 표현 가능합니다.

학생(성별, 학년, 학과)

그리고 튜플이 있는 데 이것은 어떤 테이블에서 행에 해당한다고 생각하시면 됩니다. 즉, 어떤 각 속성에 해당하는 원소 또는 실제 값들의 집합이라고 할 수 있습니다. 아래가 대표적인 테이블의 예시라고 할 수 있습니다.

Name Manufacturer
Hite Jinro
Cass OB

이러한 테이블에서 Name, Manufacturer는 속성으로 열의 헤더(header)에 해당합니다. 그리고 헤더를 제외한 각 행은 튜플을 의미합니다. 이러한 형태의 테이블의 스키마를 정의하면 Beers(Name, Mnufacturer)라고 할 수 있습니다.

관계 스키마

관계 스키마에 관해서 좀 더 알아보도록 하겠습니다. 관계 스키마에는 아래의 데이터들이 들어가야 합니다.

  • 관계 이름
  • 속성과 속성의 형 또는 순서
    (e.g. Beers(name, manufacturere) 또는 Beers(name:string, manf:string))
  • 키에 대한 정의
  • 제약조건에 대한 정의

예를 들어, 아래와 같은 클래스에 대해서 스키마를 정의하면 Movie(title, year, length, genre)가 될 수 있습니다. 여기서 밑줄이 있는 것은 해당 속성이 키(Key)라는 것을 의미합니다.

schema

왜 관계 데이터 모델을 사용하는가?

결론적으로 말하면 수학적인 배경이 있으며, 표현이 쉬우며, 물리적인 독립성을 보장해주기 때문입니다. 여기서 물리적인 독립성의 보장은 이 모델을 사용하면 SQL이라는 표준화된 언어를 사용할 수 있는 데, 이는 내부적인 구현 사항을 모르고도 어떤 DBMS에서 같게 사용할 수 있기 때문입니다.

SQL

SQL은 흔히들 “sequel” 또는 “에스큐엘”이라고 발음을 합니다. 이는 관계형 데이터베이스의 선언형 언어로 스키마를 정의하는 데 있어서 DDL(Data Definition Language) 적인 특징을 가지고, 질의(Quering)을 하는 데는 DML(Data Manipulation Language) 적인 특징을 가집니다.

이러한 SQL은 선언형 언어답게 절차를 서술하지 않고 목적만 서술하도록 합니다. 이러면 나머지는 DBMS가 알아서 최적화시켜서 데이터를 처리하도록 합니다. 결과적으로, 물리 영역에 대한 이해가 필요 없어지게 됩니다.

스키마 정의

/*           (테이블 이름)*/
CREATE TABLE Movies{
  /*(속성명)    (자료형) 형식을 따릅니다. */
    title       CHAR(100), /*한 줄이 끝나면 무조건 콤마를 붙이도록 합니다.*/
    year        INT,
    length      INT,
    genre       CHAR(10),
    studioName  CHAR(20),
    producerC#  INT,
    PRIMARY KEY (title, year) /*마지막 줄은 콤마를 생략합니다*/
    /*PRIMARY KEY 부분은 기본키를 선언하는 줄입니다.*/
};

SQL 기본 자료형

  • 문자형 : CHAR(n) 또는 VARCHAR(n), VAR가 사용한 만큼만 메모리 확보가 됩니다.
  • 비트형 : BIT(n) 또는 VARBIT(n)
  • 불리언 자료형 : BOOLEAN
  • 정수형 : INT, INTEGER 또는 SHORTINT
  • 실수형 : FLOAT 또는 REAL, DOUBLE PRECISION, DECIMAL(n,d)
  • 시간형 : DATE, TIME

SQL 추가 내용

만약 수정을 하고 싶은 경우 아래의 명령어들을 사용하면 됩니다.

DROP TABLE Movies; /* 스키마를 없애는 명령어 */
ALTER TABLE Movies ADD address CHAR(100); /* 속성을 추가하는 명령 */
ALTER TABLE Movies DROP producerC#; /* 속성을 제거하는 명령 */

또한, 이런 SQL에서도 기본 값을 줄 수 있습니다. 그 방법은 아래와 같습니다.

CREATE TABLE Movies{
    movie#      INT         PRIMARY KEY, /* 기본키가 됩니다. */
    title       CHAR(100),
    year        INT,
    length      INT,
    /* 데이터 입력이 없으면 genre는 자동으로 UNKNOWN이 됩니다. */
    genre       CHAR(10)    DEFAULT 'UNKNOWN',
    studioName  CHAR(20),
    producerC#  INT,
};

관계 대수

이제 본격적으로 관계 대수를 사용해보도록 하겠습니다. 관계 대수의 기본 폼은 아래와 같습니다.

\[Set(Operands) + Operators\]

여기서 피연산자(Operands)와 연산자(Operator)는 각각 다음을 의미합니다.

  • 피연산자 : 관계(테이블)
  • 연산자 : 관계 연산
    • 집합 연산 : 합집합, 교집합, 차집합
    • 선택(Selection)
    • 프로젝션(Projection)
    • 조인(Join)
    • 집합(Aggregate) : 테이블에 존재하는 튜플에 대한 통계를 내는 연산자입니다.

이러한 연산의 대상은 튜플 하나가 아니라 테이블 전체임을 유의해야 합니다.

선택(\(\sigma_{condition}\))

선택(Selection)은 테이블에서 특정한 조건을 만족하는 것을 뽑아내는 연산입니다. 일반적으로 B+ 트리나 동적 해시로 구현이 되어 연산을 수행하나 최악은 선형 탐색이 될 수 있는 명령입니다. 예를 들어, 학생들의 성적표(Student)에서 학점이 3.5가 넘는 학생 데이터를 추출하기 위해서는 아래와 같은 명령을 써야 합니다.

\[\sigma_{score > 3.5} (Student)\]

프로젝션(\(\Pi_{attributes}\))

프로젝션(Projection)은 테이블에서 속성(Attribute)에 해당하는 내용 전체를 뽑는 방법입니다. 전체를 뽑기 때문에 탐색 또한 전체로 수행되게 됩니다. 예를 들어, 학생들의 성적표에서 학점이 3.5가 넘는 학생들의 이름을 추출하기 위해서는 아래와 같은 명령을 써서 추출할 수 있습니다.

\[\Pi_{name} (\sigma_{score > 3.5} (Student))\]

조인(\(\Join\))

조인을 이해하기 위해서는 곱집합(Cartesian Product)에 대해서 이해해야 합니다. 곱집합은 임의의 두 관계 \(R_1\), \(R_2\)에 대해서 \(R_1 \times R_2\)로 표기할 수 있습니다. 이를 하면, 만약 \(R_1\)의 튜플이 \(10\)개이고 \(R_2\)의 튜플이 \(20\)개인 경우에 곱집합에 의해 나오는 새로운 관계의 튜플 개수는 \(10 \times 20 = 200\)이 되게 됩니다.

하지만 일반적으로 저렇게 나온 모든 결과를 사용하지는 않습니다. 저 중에서 만약 공통된 속성이 있으면 그 속성을 묶어서 추출하도록 합니다. 즉, 조인은 곱집합에서 특정 조건을 만족하는 것만 뽑는 기능을 의미합니다. 예를 들어, 학생에 관계된 어떤 스키마가 Student(StudentName, AdvisorProfessorID, Department, Score)라고 하고, 교수에 관계된 스키마가 Professor, ProfessorID, Department)라고 하도록 하겠습니다. 여기서 AdvisorProfessorID와 ProfessorID는 겹쳐지는 속성입니다. 따라서, 이 값이 같은 튜플끼리 합치도록 아래의 명령어를 써 주도록 합니다.

\[Student \Join_{AdvisorProfessorID=ProfessorID} Professor\]

이 말은 다음과 같습니다.

\[\sigma_{AdvisorProfessorID=ProfessorID} (Student \times Professor)\]

그리고 이러한 조인에는 자연(Natural) 조인과 세타(Theta) 조인이 있습니다. 자연 조인은 위에서 나오듯이 공통된 속성에 대해서 조인을 해주는 것을 지칭합니다. 이에 반해, 세타 조인은 실질적인 조건(e.g. A는 B보다 크다)이 들어가서 조인을 하는 것을 지칭합니다.

또한, 이러한 조인에는 매우 많은 시간이 필요할 수 있습니다. 따라서, 이 연산을 할 때는 그러한 것을 염두에 두고 수행을 하도록 해야 합니다.

다음은 실질적인 조인을 하는 과정과 관계된 그림이고, 이것을 통해 위의 내용을 좀 더 이해하기가 쉬울 것입니다.

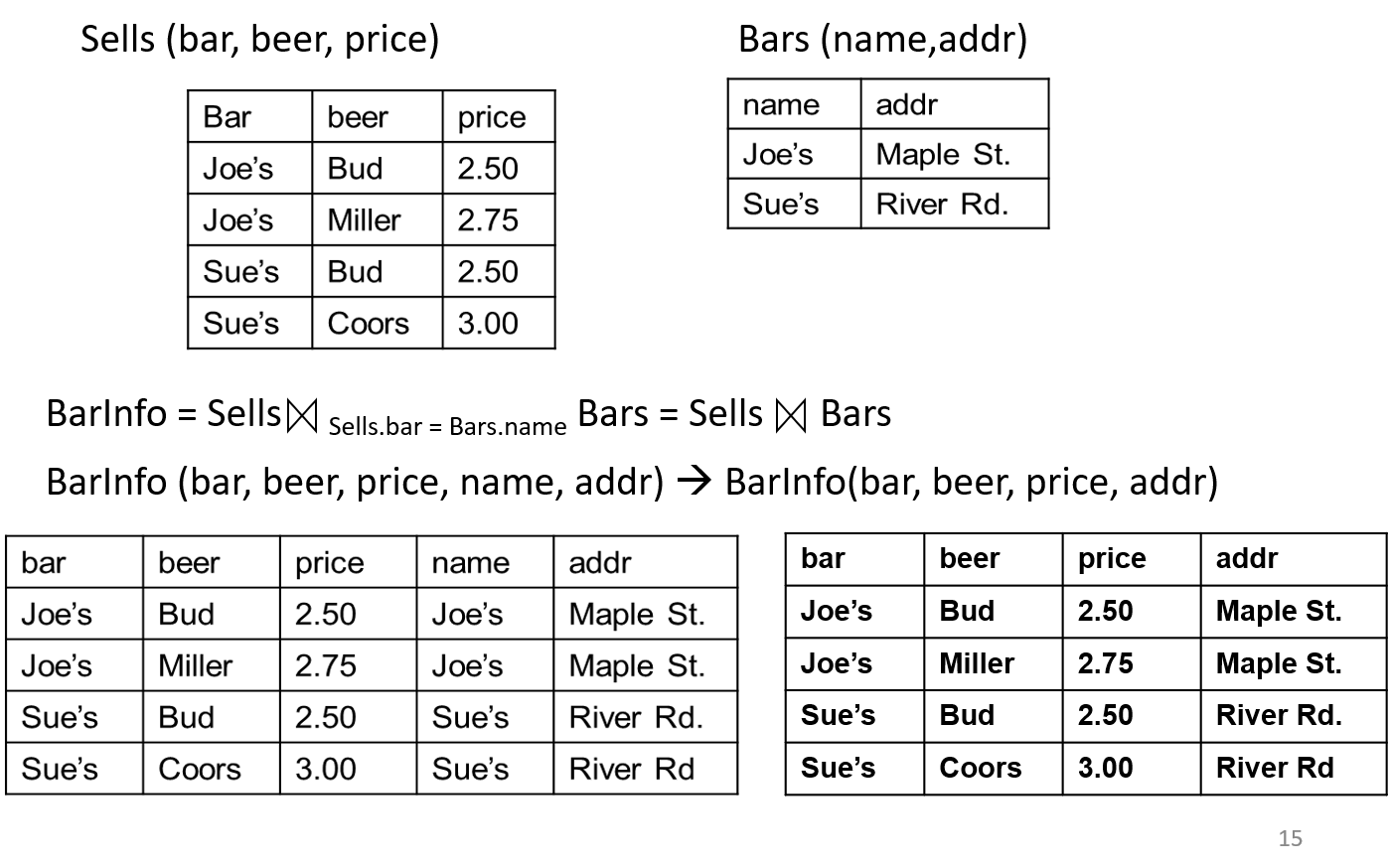
cartesian!

관계 대수 추가 내용

위의 다양한 관계 대수를 보았습니다. 여기서 “지도교수의 학과가 컴퓨터공학과이고 학생 학점이 3.5 초과인 학생을 찾아라!”라는 문장을 질의문(Query)이라고 합니다. 이런 질의에 대해서 여러 개의 연산자를 복합적으로 이용해서 데이터를 찾는 과정을 적은 식을 보고 관계식이라고 합니다. 그리고 이러한 관계식을 쓰는 이유는 다른 방법에 비교해 컴퓨터가 좀 더 쉽게 계산할 수 있기 때문입니다.

이러한 관계식은 한 가지로만 표현되지 않습니다. 이를테면, 위에서 나온 질의문을 관계식으로 표현하면 아래와 같이 작성할 수 있습니다. 단, 자연 조인은 명확하게 대응하는 것이 어떤 것인지 알 수 있으므로 따로 적지 않도록 하겠습니다.

\[\Pi_{student.name}(\sigma_{score>3.5}(Student) \Join \sigma_{Department=’CSE’} (Professor))\]

이를 다르게 표현하면 아래와 같이 표현도 가능합니다.

\[\Pi_{student.name}(\sigma_{Student.score>3.5 and Professor.Department=’CSE’}(Student \times Professor))\]

이를 보고 동치(Equivalent)라고 합니다. 이러한 동치를 하는 이유는 두 연산 중에 좀 더 컴퓨터에서 빨리 해석되는 연산을 찾기 위함이고, 빨리 해석되는지 알아보는 방법은 비용 예측을 통해서 확인이 가능합니다. 이는 질의 전처리기로 최적화가 됩니다.

관계 제약조건

이러한 관계 연산에도 제약조건을 줄 수 있습니다. 이를테면, 아래의 경우를 생각해보도록 하겠습니다.

uni

각각의 스키마가 Student(name, ID, dept, score), Department(name, college, office)라고 하는 경우에 위의 UML 다이어그램에 대한 관계식은 아래와 같이 작성할 수 있습니다.

\[\Pi_{dept} (Student) \subseteq \Pi_{name} (Department)\]

또는 다음과 같은 방식으로도 작성 가능합니다.

\[\Pi_{dept} (Student) - \Pi_{name} (Department) = \emptyset\]

키 제약조건

테이블에서 하나 이상의 속성이 키(Key)로 존재하여 각각의 튜플을 분류할 수 있게 되어야 합니다. 이러한 제약조건의 작성은 아래와 같은 방식으로 작성 가능합니다.

만약 ID가 Student의 키 속성이라면 \(\rho_{Stud1} (Student)\), \(\rho_{Stud2} (Student)\)에 대해서 \(\sigma_{Stud1.ID=Stud2.ID and Stud1.dept \neq Stud2.dept} (Stud1 \times Stud2) = \emptyset\)을 만족한다.

즉, 이 말은 키가 같은 데 속성이 다른 경우가 없음을 의미합니다. 근데 여기서 \(\rho_{Stud1} (Student)\)가 나오는 데 이것은 어떤 Student라는 이름의 테이블의 이름을 Stud1로 변경하겠다는 것을 의미합니다.


database Share Tweet +1