출처 : Willian Stallings. (2013). Computer Organization and Architecture. London:Pearson
Computer Arithmetic
컴퓨터는 애초에 수학적 연산을 좀 더 쉽게 하기위해 나왔습니다. 따라서 이런 수학적인 연산과 관련한 정의가 매우 중요합니다. 이런 연산을 하는 데 사용하는 모듈을 ALU(Arithmetic Logic Unit)라고 합니다. 이러한 ALU는 일반적으로 아래와 같은 모형을 하고 있습니다.

정수의 표현
정수를 표현할 때에는 2진법으로 표현을 하도록 합니다. 하지만 이러한 이진법으로 표현을 하게되면 음의 값의 표현을 할 수 없게 됩니다. 따라서, 부호 절대값 표기법(Sign-Magnitude)과 2의 보수법(Two’s completemt) 방법을 사용해서 음의 값을 표현하는 방법을 보도록 하겠습니다.
부호 절대값 표현
이 방법은 가장 좌측에 있는 비트(이하 MSB1)를 부호 비트로 설정해서 사용하는 방법입니다. 이 비트의 값이 0이면 양수를 1이면 음수를 의미합니다.
\[+18 = 00010010_{(2)}\] \[-18 = 10010010_{(2)}\]하지만 이 방법은 2가지 문제를 가지고 있습니다.
- 산술 계산을 하는 데 있어서 부호와 절대값 둘 다를 알 필요가 있습니다.
- 0을 표현하는 데 2개의 표현 방법이 있습니다. (+0, -0)
특히, 여기서 2번 문제는 꽤 중요한 문제입니다. 이 문제를 해결하기 위해서 2의 보수법이 나오게 되었습니다.
2의 보수법
이 방법은 음수를 만들기 위해서는 기존의 양수 값에다가 1의 보수2를 취하고 그 값에다가 1을 더해주는 방식입니다. 예를 들어 아래와 같이 구성될 수 있습니다.
\[+3 = 00000011_{(2)}\] \[0 = 00000000_{(2)}\] \[-3 = 11111101_{(2)}\]이 방법의 장점은
- 0의 표현이 한 가지만 존재한다.
- 산술 계산이 쉽게 일어납니다.
- 음수로 만드는 방법이 쉽습니다.
주의 사항으로 2의 보수가 만족을 하기 위해서는 필히 오버플로우(overflow) 되는 값은 고려되지 않는다는 전제 조건이 있어야 합니다. 이를 보고 비트가 특정되어야 한다고 합니다. 이렇게 비트가 특정되지 않는다면 2의 보수는 유효할 수 없게 됩니다. 이런 조건으로 인해 2의 보수의 표현 범위는 한정됩니다. 따라서 \(n\) 비트에서의 2의 보수 표현의 최대 범위는 \(-2^{n-1} \sim 2^{n-1} - 1\)이 범위가 됩니다.
그리고 이러한 2의 보수 값에 대해 비트 확장이 벌어지면 MSB의 값으로 확장이 됩니다. 예로서 내용을 알아보도록 하겠습니다.
\[+18 = 0001 0010\] \[+18 = 0000 0000 0001 0010\] \[-18 = 1110 1110\] \[-18 = 1111 1111 1110 1110\]이런 식으로 발생을 하게 됩니다.
그렇다면 하드웨어적으로 어떻게 제작을 하는가? 다음과 같이 제작을 할 수 있습니다.
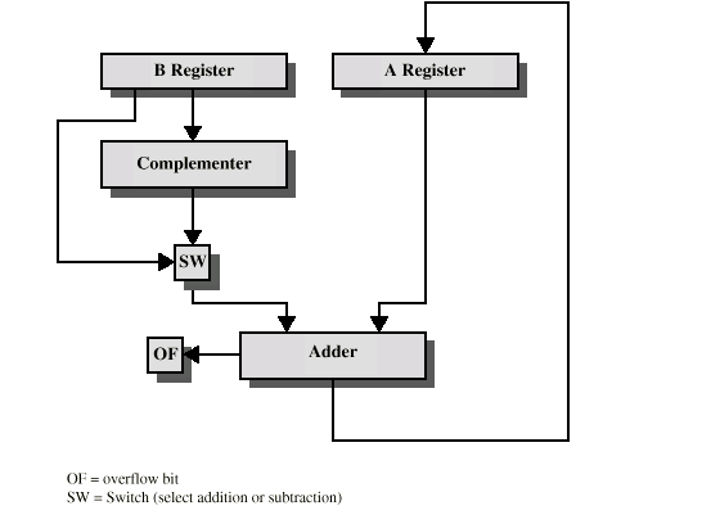
여기서 중요한 것은 SW입니다. 이 스위치에 의해서 2의 보수가 수행되게 됩니다.
곱셈
컴퓨터에서의 곱셈은 복잡한 작업입니다. 이를 하는 방법은 부분적으로 자릿 수마다 곱셈을 하는 방법으로 해결하도록 합니다. 단적인 곱셈의 예입니다.

이 방법을 블럭 다이어그램으로 구현을 하면 아래와 같이 나타납니다.
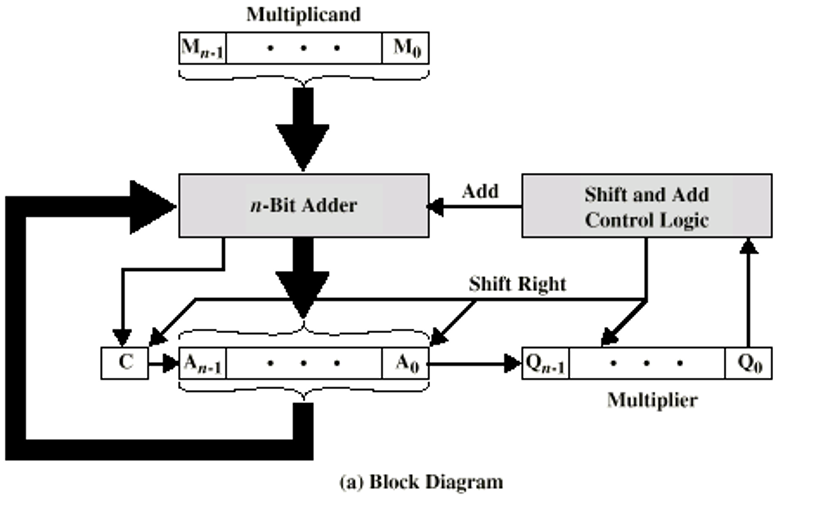
그리고 이것의 실행은 다음과 같이 됩니다.

여기서 C는 Overflow된 비트가 들어갑니다. 그리고 A는 Partial pruduct를 의미하고, Q는 Multiplier를 M은 Multiplicand를 의미합니다. 여기서 add를 실행하는 경우는 Q의 비트가 1인 경우에만 실시하도록 합니다. 그리고 shift는 \(\{C \| A \| Q\} >> 1\) 이 됩니다. First Cycle을 바탕으로 확인을 하면, First Cycle Add에서 \(\{C \| A \| Q\}\)는 0 1011 1101이 됩니다. 이 값을 그냥 그대로 right shift를 실시하면 shift가 됩니다. 이런 방식은 매우 유용합니다. 하지만 한 가지 문제가 있는 데 이 방식은 음수 곱셈에서는 적용되지 않습니다. 이 방법을 해결하기 위해서 새로운 해결책이 2가지가 나왔습니다.
- 양수로 바꿔서 계산을 한 후에 결과의 부호를 조사해서 양수 또는 음수로 만들어주도록 한다.
- Booth의 알고리즘을 사용하도록 한다.
Booth의 알고리즘
Booth의 알고리즘은 다음과 같이 돌아갑니다.
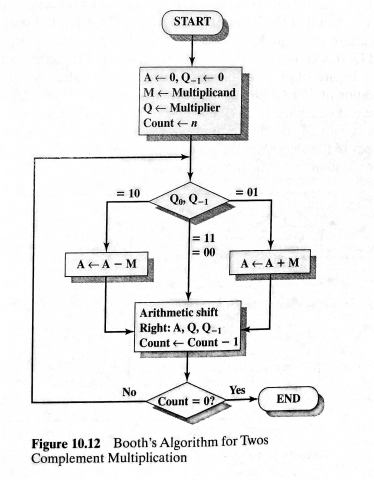
여기서는 앞에서 \(\{C \| A \| Q \}\)가 \(\{A \| Q \| Q_{-1}\}\)이 됩니다. 여기서 주의해서 봐야할 값으로는 Q의 제일 우측에 있는 값인 \(Q_0\)랑 \(Q_{-1}\) 입니다. 이들의 값이 어떻게 되냐에 따라서 그 음수냐 양수냐가 계산이 됩니다.
| \(Q_0\) | \(Q_{-1}\) | \(Q_{-1} - Q_0\) | 명령 |
|---|---|---|---|
| 0 | 0 | 0 | 아무일도 하지 않습니다 |
| 1 | 0 | -1 | 부분 곱에서 M을 빼주도록 합니다. |
| 1 | 1 | 0 | 아무일도 하지 않습니다 |
| 0 | 1 | 1 | 부분 곱에서 1일 더해주도록 합니다. |
그럼 아래와 같이 계산이 일어나게 됩니다.
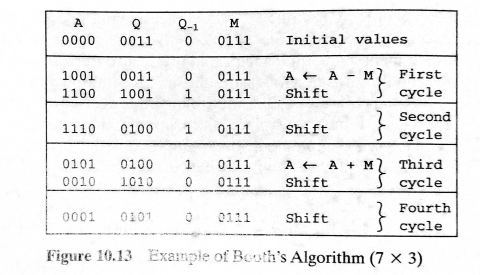
이와 같은 방법을 통해서 음수의 곱도 완료했습니다.
나눗셈
곱셈보다 더 구현이 힘듭니다. 이것은 아래의 순서도와 같이 돌아가게 됩니다.
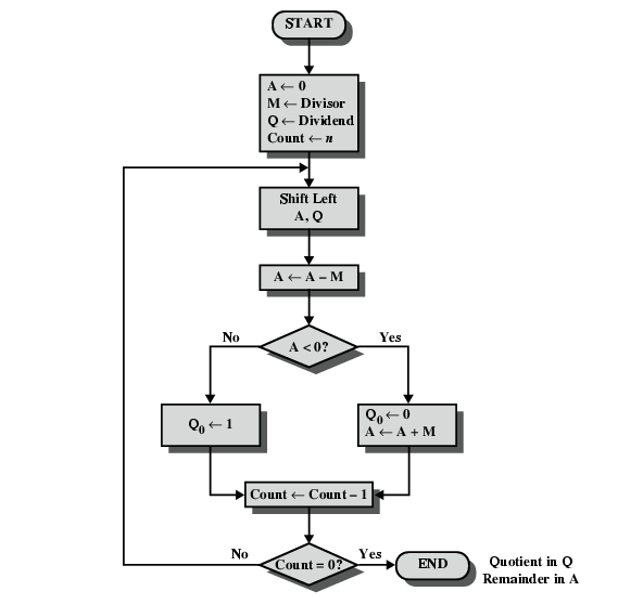
실수
이진법의 실수는 다음과 같은 방식으로 계산이 됩니다.
\[-1001.1010 = 2^3 + 2^0 + 2^{-1} + 2^{-3} = 9.625\]이런 실수를 컴퓨터에서 표현하는 데에는 고정 소수점(Fixed Point) 방식이 있고, 부동 소수점(Floating Point) 방식이 있습니다. 하지만 고정 소수점의 경우 그 표현가 계산이 매우 복잡하기 때문에 매우 제한적으로만 이용을 하고, 현재의 기본적인 실수 표현 방법은 부동 소수점 표현 방법입니다.
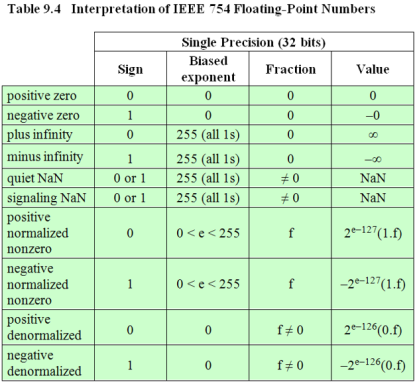
부동 소수점 표현 방법은 아래와 같이 구성됩니다.
여기서 보이듯이 부호부(sign)와 지수부(exponent), 가수부(fraction)로 구성이 되어있습니다. 수학적으로 표현을 하면 아래와 같이 나타낼 수 있습니다.
\[x = \pm(.fraction) \times 2^{exponent}\]또한 저기서 지수부는 Excess 127을 사용합니다. 이를 사용하는 이유는 지수부에서의 음수 표현을 위해서입니다. 따라서, 지수부의 범위는 8비트 기준으로 기존 0 ~ 255에서 127을 뺀 값인 -127 ~ 128이 표현 가능한 값이 됩니다. 하지만 이런 방식으로만 만든다면 32비트 컴퓨터에서 8비트 지수부에 23비트 가수부에 따라서 음수의 범위는 \(-(2-2^{-23}) \times 2^{128} \sim -2^{-127}\)이고, 양수의 범위는 \(2^{-127}\sim (2-2^{-23}) \times 2^{128}\)이 됩니다. 여기서 우리는 이 표현법으로는 0을 표현할 수 없다는 것을 알게 되었습니다. 이러한 문제점을 해결하기 위해 IEEE3에서 표준을 만들었습니다. 이것이 IEEE 754이고 이것은 아래와 같은 포맷을 가집니다.