유도

유도(derivation)는 생성규칙에 대한 응용을 의미합니다. 수학적으로는 문법 기호로 구성된 문자열(\(N \cup T\))들의 관계를 의미합니다. 그러므로 유도는 폐쇄(closure)의 확장이라고 할 수 있습니다.

그리고 유도에서의 비결정적(non-determinism)인 사항에 관해서 알아보도록 하겠습니다. 모든 유도과정에 있어서 우리는 논 터미널을 자유롭게 선택을 할 수 있습니다. 이것은 문자열을 생성하는 데 매우 좋은 방법이나 문자열의 구조를 이해하는 데에는 좋지 않은 방법입니다. 따라서 우리는 문자열을 위한 독특한 구조를 필요로 합니다.

최좌단 또는 최우단

아래의 문법을 생각해봅시다.

E ::= E + E | E - E | N
N ::= "0"|"1"

이 문법에 대해서 만약 우리가 매 유도과정에서 최좌단(leftmost)의 논 터미널을 선택한다면 이를 최좌단 유도라고 합니다. 반대의 최우단(rightmost)도 같습니다. 최좌단 유도일 때 \(\Rightarrow_{lm}\)을 최우단 유도일 때 \(\Rightarrow_{rm}\)이라고 하도록 합니다. 하지만 이를 일일이 표현하기로는 어려우므로 이 글에서는 생략하고 상단에 이를 명시하는 식으로 하여 작성하겠습니다.

위 내용을 바탕으로 위에서 나타난 문법을 \(1+0-1\)에 먼저 최좌단 유도를 시키도록 하겠습니다.

E => E + E => E + E - E => N + E - E => N + N - E => N + N - N

이번에는 최우단 유도를 시키도록 하겠습니다.

E => E - E => E + E - E => E + E - N => E + N - N => N + N - N

파스 트리

하지만 최좌단 및 최우단 유도만으로 구조의 독특한 구조를 결정하기에는 충분하지 않습니다. 그리고 유도의 최좌단 유도(최우단 유도)가 같은 구조인지를 표현하지 못하고 있습니다. 그래서 나온 게 파스 트리(parse tree)입니다. 이는 트리로 표현되는 유도의 일련(一連)입니다. 이러한 트리는 보통 유도 트리 또는 파스 트리라고 하며 파스 트리에서의 유도 순서는 그렇게 큰 상관을 쓸 필요가 없습니다.

위에서 나온 문법에 \(1 + 0 - 1\)에 대한 파스 트리를 구성해보도록 하겠습니다.

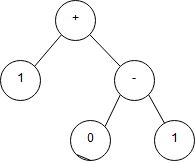
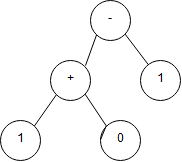
여기서 상단의 트리는 최좌단 유도에 해당하는 트리이고, 하단의 트리는 최우단 유도에 해당하는 트리입니다. 보다시피 하나의 내용에 대해서 2개의 트리가 만들어지는 상황이 벌어지고 있습니다. 이에 관해서 이제 알아보도록 하겠습니다.

모호성

문자열 \(x \in L(G)\)를 만족하는 문법 \(G\)에 대해서 1개 이상의 파스 트리가 만들어지면 ‘모호하다(ambiguous)’라고 말합니다. 이러한 모호성은 컴퓨터의 내용 판단에 많은 어려움을 줌으로 없애야 합니다. 그렇다면 위의 문법을 모호성 제거 규칙(disambiguating rules)을 주어서 모호성을 없애도록 하겠습니다.

E -> E + N | E - N | N
N -> "0" | "1"

이렇게 할 때 모호성이 사라집니다. 먼저 최좌단 유도를 하는 경우 아래와 같이 됩니다.

E => E - N => E + N - N => N + N - N

이번에는 최우단 유도의 경우입니다.

E => E - N => E + N - N => N + N - N

이제 최좌단 유도와 최우단 유도는 같은 과정을 보임을 알 수 있습니다. 이에 대한 파스 트리는 아래와 같이 될 것입니다.

이번에는 또 다른 상황을 보도록 하겠습니다.

E -> E + N | E * N | N
N -> "0" | "1"

이런 경우 모호성은 없습니다. 하지만 \(1+1*0\)과 \(1*0+1\)의 파스 트리를 구축해보도록 하면 우측은 수학적 규칙에 맞게 결과를 도출할 수 있지만, 좌측의 값은 전혀 이상한 결과를 출력하게 됩니다. 실제로 좌측의 내용을 유도하면 아래와 같은 파스 트리가 만들어집니다.

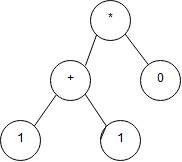
보면 아시겠지만 \(1+1\)이 하나의 서브 트리로 먼저 계산이 되고 \(\times 0\)이 됨을 알 수 있습니다. 이를 해결하기 위해서는 곱셈 연산의 우선순위를 주는 서브 트리를 생성하는 규칙을 만들어주어야 합니다. 이를 보고 우선순위 캐스케이딩(precedence cascading)이라고 합니다. 이러한 생각을 바탕으로 규칙을 만들면 아래와 같이 구성 가능합니다.

E -> E + T | T
T -> T * N | N
N -> "0" | "1"

이 경우, 파스 트리 유도과정은 아래와 같습니다.

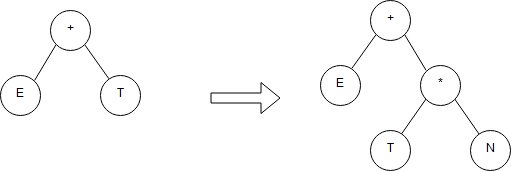
이렇게 하면 순서가 바뀐다고 해도 우선순위가 먼저인 내용은 따로 서브 트리가 생성되게 만들 수 있습니다.